立候補者の知名度差および組織票の影響を軽減する零和投票方式について

時事雑談
21

なるほど〜
複数の候補者へのマイナス票が組織的かどうかまで判断することは原理的に可能なんですかね？

今、固有ベクトル中心性のアイデアから一旦離れて、候補者の序列を仮定したときにその序列が自身の投票に則したものになっているような有権者の数が最大となるような序列を選挙結果とするシステムならどうかを検討しています。

例えば5人の候補者の序列がA>B>C>D>Eであると仮定したときは、DさんからCさんに票を移動した有権者やEさんからAさんに票を移動した有権者は“序列が自身の投票に則したものになっている有権者”としてカウントしますが、逆にCさんからDさんに票を移動した有権者やAさんからEさんに票を移動した有権者などはカウントしないといった具合です。

まだ、妥当性については結論が出ていませんが・・。

22

うーん、結構難しそう
特に昨年の石丸ブームのように例年通りじゃないけど、組織票ではないこともあるから

「いいね！」 1
23

固有ベクトル中心性に関しては

A = [
[0, 0.31, 0.20, 0.10, 0.20],
[0.18, 0, 0.90, 0.85, 0.80],
[0.22, 0.88, 0, 0.83, 0.80],
[0.15, 0.87, 0.84, 0, 0.92],
[0.25, 0.81, 0.79, 0.88, 0]
]

これだと、

Figure_1
Figure_1640×480 25.5 KB

候補者0（無名枠）は落選するのに対して、

A = [
[0, 0.30, 0.20, 0.10, 0.20],
[0.19, 0, 0.90, 0.85, 0.80],
[0.22, 0.88, 0, 0.83, 0.80],
[0.15, 0.87, 0.84, 0, 0.92],
[0.25, 0.81, 0.79, 0.88, 0]
]

と、A[0][1]を0.01減点し、A[1][0]を0.01加点した場合、

Figure_1(1)
Figure_1(1)640×480 22.8 KB

候補者0が当選するというバグが発生する気がする

「いいね！」 1
24

みなさん、これについてはどう思いますか？

25

現在までの議論をもとに、AIによる意見まとめが生成されました！
ぜひ見てみてくださいね。

特に「選挙シミュレーションにおいて、現実の選挙における競争状況（資金力、組織力など）をどの程度反映させるべきか？」という点について、特に多様な意見が出ているようです。

新たな論点

選挙シミュレーションにおいて、現実の選挙における競争状況（資金力、組織力など）をどの程度反映させるべきか？

1. 現実反映重視派：選挙リアリズム探求者

このスタンスでは、現実の選挙における競争状況を積極的に反映し、よりリアルな結果を目指します。資金力、組織力、戦略といった要素を重視し、有権者の多様な要素に基づく投票行動をシミュレーションに組み込みます。

メリット: より現実的な結果が得られ、選挙結果の予測精度が向上する可能性があります。
デメリット: 競争状況の正確なデータ収集が困難であり、シミュレーションの複雑性が増す可能性があります。また、不公平感を助長する可能性も考慮する必要があります。

2. 中立性重視派：理想的投票追求者

このスタンスでは、選挙シミュレーションの中立性を最優先し、競争状況の影響を最小限に抑えることを目指します。公平な条件でシミュレーションを行い、有権者の投票行動の分析に特化することで、客観的な結果を追求します。

メリット: 特定の候補者に有利不利が生じない、公平なシミュレーションが可能です。
デメリット: 現実の選挙との乖離が生じ、シミュレーション結果の解釈に注意が必要です。

3. 段階的反映派：バランス型選挙分析者

このスタンスでは、中立性を重視したシミュレーションを行い、その上で、競争状況の影響を段階的に加えていく方法を検討します。競争状況の反映度合いを調整可能なシミュレーションモデルや、現実の選挙結果を参考にシミュレーション結果を調整する手法も有効と考えます。

メリット: 現実性と公平性のバランスを取り、多様な視点からの分析が可能です。
デメリット: シミュレーションモデルの複雑性が増し、パラメータ調整の難易度が高くなる可能性があります。

上記3つのスタンスは、それぞれ異なる利点と課題を持っています。どのオプションを選ぶかは、シミュレーションの目的や重視するポイントによって変わってくるでしょう。たとえば、シミュレーションの目的が「選挙結果の予測」であれば現実反映重視派が、
「候補者の政策比較」であれば中立性重視派が、といったように使い分けることも考えられます。

リソースには限りがあるという前提で、まず始めるならどのスタンスでシミュレーションを行うのが良いでしょうか？

上記を参考に、あなたの意見を教えて下さい！

この3つのスタンス以外にも、選挙シミュレーションに対する様々なアプローチが考えられます。あなたのユニークな視点もぜひ聞かせてください！

26

無名候補者問題は解決できなさそう
組織票に関しては考えるのに時間がかかるから時間経ったら返信します

「いいね！」 1
27

クアドラティックゼロサムボーティングってどうですか?

  1. まず、99クレジットで候補者から票を奪う
  2. クレジット数がマイナスになるので、0になるように他の候補者に入れる
「いいね！」 1
28

いろいろな投票法があるんですね。とりあえず票移動方式で考えてみました。
どういう投票パターンが、もし知名度があったら、多くの票数になる可能性があるのかを考えてみました。特定候補者から、票が移動しているより、多くの候補者から、票が移動している人のほうが、知名度があがれば、票が増えると考えました。その場合、グラフ理論のなかでは、ページランクという指標があっていそうです。
投票パターンを
[[0, 5, 5, 0, 0],
[5, 0, 3, 0, 0],
[4, 2, 0, 0, 0],
[3, 0, 0, 0, 0],
[1, 1, 1, 0, 0]]
（横方向の和が加算される票(プラス票)、縦方向の和が減算される票(マイナス票)）
として、固有ベクトル中心性と、ページランクを比較してみました。

output_0_0
output_0_0660×522 29 KB

output_0_3
output_0_3547×435 8.63 KB

output_0_4
output_0_4556×435 4.67 KB

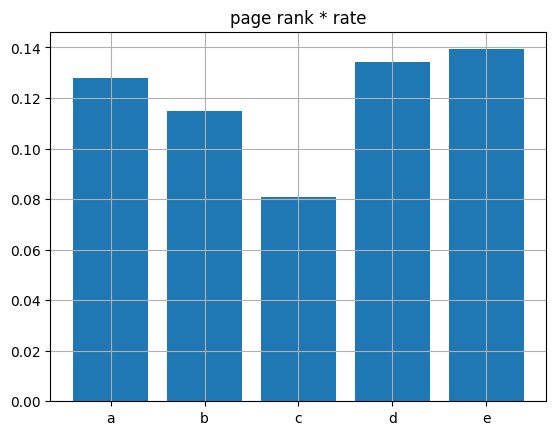
候補者dは候補者aからのみ票が移動していませんが、候補者eは候補者a,b,cから票が移動しています。なので、固有ベクトル中心性では候補者eが最下位ですが、ページランクでは候補者dが最下位になっています。絶対的票数がすくないと、上位にはならないです。ページランクにプラス票 / (プラス票 + マイナス票)をかけることを考えました。マイナス票が少ないほうが有利になるように考えました。
output_0_5
output_0_5556×435 4.56 KB

今回の例では、候補者d,eはマイナス票は０なので、いっきに1,2位に上がっています。当選者は候補者eになります。多くの候補者から票がきていて、嫌われていないということなで、いろいろな層から支持され、知名度があれば票数が増える候補者が選ばれたと考えられませんでしょうか？今回の例はかなり恣意的に投票パターンを決めているので、実際にどうかは、もっと検討が必要だとはおもいますが。
一応計算に使用舌コードを記載しておきます。networkxで計算しています。

import numpy as np
import matplotlib.pyplot as plt
import networkx as nx

# グラフ表示
def calculate_eigenvector_centrality(graph):

    # グラフの描画
    # pos = nx.spring_layout(graph)
    pos = nx.circular_layout(graph)
    nx.draw(graph, pos, with_labels=True, node_color='lightblue', node_size=500, edge_color='gray', arrows=True)

    # 辺の重みを表示 (両方向を区別)
    edge_labels = {}
    for u, v, data in graph.edges(data=True):
        edge_labels[(u, v)] = data['weight']
        if (v, u) in graph.edges():
            edge_labels[(u, v)] = f"{data['weight']}/{graph[v][u]['weight']}" # 両方向の重みを表示
    nx.draw_networkx_edge_labels(graph, pos, edge_labels=edge_labels)

    plt.title("Weighted directed graphs")
    plt.show()

# main ------------------------------
# 票の移動量設定
A = np.array([
[0, 5, 5, 0, 0],
[5, 0, 3, 0, 0],
[4, 2, 0, 0, 0],
[3, 0, 0, 0, 0],
[1, 1, 1, 0, 0]
])
num, _ = A.shape

# 候補者名
cname = ['a', 'b', 'c', 'd', 'e']

# for networkX
G = nx.DiGraph()
for i in range(num):
    for j in range(num):
        if i!=j:
            G.add_edge(cname[i], cname[j], weight=A[j, i])

in_degree = G.in_degree(weight='weight')
out_degree = G.out_degree(weight='weight')
dout_degree = dict(out_degree)
name = []
sum01 = [] # プラス票の総和
sum02 = [] # プラス票 - マイナス票
rate = {} # プラス票/(プラス票 + マイナス票)
for key, value in in_degree:
    name.append(key)
    sum01.append(value)
    sum02.append(value-dout_degree[key])
    rate[key] = np.double(value)/np.double(value+dout_degree[key])

# 固有ベクトル中心性計算
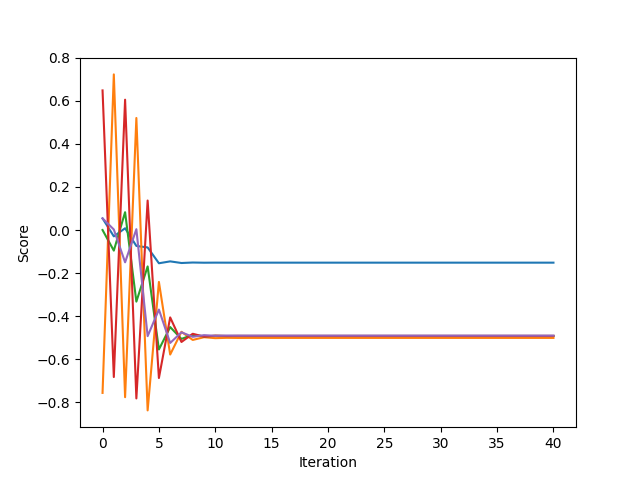
eigenvector_centrality = nx.eigenvector_centrality(G, weight='weight')
# ページランク計算
pagerank = nx.pagerank(G, weight='weight')
# ページランク * プラス票 / (プラス票 + マイナス票) 計算
pagerankrate = {}
for key, value in pagerank.items():
    pagerankrate[key] = pagerank[key]*rate[key]

# 図表示
calculate_eigenvector_centrality(G)

plt.bar(name, sum01)
plt.grid()
plt.title('sum')
plt.show()
plt.bar(name, sum02)
plt.grid()
plt.title('Addition and subtraction')
plt.show()
plt.bar(eigenvector_centrality.keys(), eigenvector_centrality.values())
plt.grid()
plt.title('eigenvector centrality')
plt.show()
plt.bar(pagerank.keys(), pagerank.values())
plt.grid()
plt.title('page rank')
plt.show()
plt.bar(pagerankrate.keys(), pagerankrate.values())
plt.grid()
plt.title('page rank * rate')
plt.show()
「いいね！」 2
29

有名候補Aと無名候補Bがいるとして（他にも沢山候補がいるとする）有名候補Aにプラス票を入れる人はマイナス票を他の有名候補にいれる可能性が十分に高いのに対して、無名候補Bにプラス票を入れる人は有名候補Aにマイナス票を入れる可能性があるリスクがありそうと思いました。

「いいね！」 2