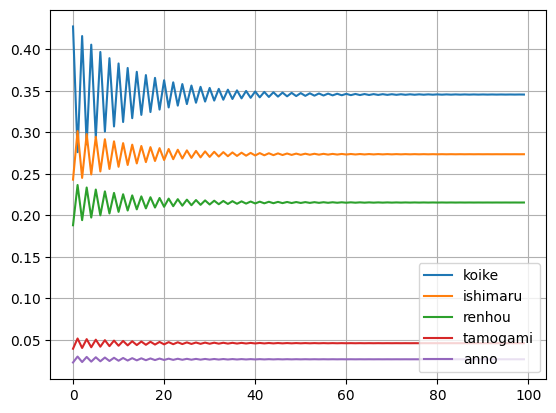
前回の都知事選の得票数を使ってシミュレーションしてみました。
票の移動は、下記の様に設定しました。
koikeさんに投票した60%がrenhouさんから、40%がishimaruさんから移動。
ishimaruさんに投票した90%がkoikeさんから、10%がrenhouさんから移動。
renhouさんに投票した90%がkoikeさんから、10%がishimatruさんから移動。
他の候補者に投票した人は100%がkoikeさんから、各候補者に移動。
import numpy as np
import matplotlib.pyplot as plt
# 得票率計算
def calVotes(A, tnum):
num, _ = A.shape
votes = np.ones(num)
p = np.zeros(num)
votes_log = np.zeros((tnum, num))
for t in range(tnum):
p = A@votes
sum_p = sum(p)
votes = p/sum_p
p = votes
votes_log[t, :] = votes
return(votes_log)
# 2024年都知事選挙 候補者名
cname = ['koike', 'ishimaru', 'renhou', 'tamogami', 'anno', 'utsumi', 'himasora', 'ishimaru', 'sakurai',
'shimizu', 'dokutaanakamatsu', 'yamato', 'kobayashi', 'gotou', 'kimiya', 'fukumoto', 'eiaimeiyaa', 'naitou',
'yokoyama', 'uchino', 'kawai', 'kougo', 'kurokawa', 'kuwahara', 'fukunaga', 'nomaguchi', 'sawa', 'ushikubo',
'komatsu', 'endou', 'ninomiya', 'takemoto', 'akinorishougunmiman', 'onodera', 'yamada', 'kimura', 'shindou',
'nakae', 'katou', 'kagata', 'katou', 'hokari', 'maeda', 'kusao', 'fukuhara', 'takeuchi', 'ozeki', 'inubuse',
'kuwajima', 'matsuo', 'furuta', 'funahashi', 'miwa', 'tsumura', 'minami', 'jouraku']
# 2024年都知事選挙 得票数
vote = [2918015, 1658363, 1283262, 267699, 154638, 121715, 110196, 96222, 83600, 38054, 23825, 9685,
7408, 5419, 4874, 3245, 2761, 2339, 2174, 2152, 2035, 1951, 1833, 1747, 1281, 1240, 1232, 1153, 894,
882, 833, 812, 792, 759, 691, 676, 669, 612, 588, 578, 572, 560, 521, 481, 466, 446, 417, 371, 361, 351,
343, 329, 306, 302, 297, 211]
num = len(vote)
tnum = 100
# 票の移動量設定
A = np.zeros((num, num))
A[0,1] = vote[0]*0.4 # ishimaru -> koike 40%
A[0,2] = vote[0]*0.6 # renhou -> koike 60%
A[1,0] = vote[1]*0.9 # koike -> ishimaru 90%
A[1,2] = vote[1]*0.1 # renhou -> ishimaru 10%
A[2,0] = vote[2]*0.9 # koike -> renhou 90%
A[2,1] = vote[2]*0.1 # ishimaru -> renhou 10%
A[3:num, 0] = vote[3:num] # koike -> each Candidates 100%
# 得票率計算
v_log = calVotes(A, tnum)
# 結果表示
plt.plot(v_log[:, :5])
plt.legend(cname[:5], loc='lower right')
plt.grid()
plt.title('Convergence of vote share')
plt.ylabel('Vote share')
print('候補者名 ', cname[:5])
print('最初の得票率[%]', v_log[0, :5]*100)
print('票の移動も考慮した得点[%]', v_log[tnum-1, :5]*100)
結果
候補者名 [‘koike’, ‘ishimaru’, ‘renhou’, ‘tamogami’, ‘anno’]
最初の得票率[%] [42.76583933 24.30463367 18.80722906 3.92334255 2.26634334]
票の移動も考慮した得点[%] [34.55931077 27.36789452 21.54806788 4.59076591 2.65188461]
票の移動はishimaruさんに有利な設定と思われますが、逆転までには至らなかったです。今回のアルゴリズムでは、そこそこ競っていないと逆転は難しいようです。嫌われない人が有利なので、現職より新人が有利になると考えられるので、そこは良いかなと思います。